VP |
30-29 |
28-27 |
26 |
25-24 |
23 |
22-21 |
20 |
19-18 |
17 |
16-15 |
14 |
13-12 |
11-10 |
9-8 |
7-6 |
5-0 |
|
NP |
15 |
14 |
13 |
12 |
11 |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
Klausur Nr. 1 Kurs 12
Pflichtteil ohne Formelsammlung und GTR:
1) Leiten Sie ab. Beachten Sie dabei die Definitionsbereiche.
a) 
2P b) 
3P
c) 
; t ¹ 0 3P
2) Gegeben ist die Funktion f mit
.
a) Zeigen Sie mittels
Polynomdivision, dass y = 
x + 1 die schiefe Asymptote des
Schaubildes
dieser Funktion ist (d.h. für x 
nähert sich das
Schaubild von f
dieser Geraden an.) . 2P
b) Prüfen Sie formal, ob das Schaubild dieser Funktion punktsymmetrisch ist zu
P( 2 ï 1 ). 3P
Wahlteil mit Formelsammlung und GTR:
3) Gegeben ist die Funktion f mit
.
a) Bestimmen Sie mit und ohne GTR die Nullstellen dieser Funktion.
(einfachste Wurzelwerte und gekürzte Brüche genügen.)
Vergleichen Sie beide Ergebnisse. 4P
b) Bestimmen Sie mit dem GTR den Wendepunkt dieser Funktion.
(erforderliche Genauigkeit: zwei Stellen hinter dem Komma,
geben Sie bitte in Kurzform Ihre Menüeingaben an, Ablesen genügt nicht) 3P
4) In einen Behälter in Form eines auf seiner Spitze stehenden senkrechten Kreiskegels
mit dem Radius R = 20 cm und der Höhe H = 60 cm werden pro Sekunde 40 cm3
Wasser gefüllt. Die Höhe des Wasserspiegels und das Volumen des Wassers im
Behälter hängen also von der Zeit t ab.
(Skizze empfehlenswert, GTR optimal einsetzen und umformen nur dort, wo unerlässlich;
erforderliche Genauigkeit: zwei Stellen hinter dem Komma, geben Sie bitte in Kurzform
Ihre Menüeingaben an)
a) Wann ist der Behälter voll? 3P
b) Ermitteln Sie
eine Zuordnung h(t) 
V(t). 2P
c) Nach wie vielen Sekunden steht das Wasser 10 cm hoch? 2P
d) Während des
Füllvorgangs steigt der Wasserspiegel unterschiedlich schnell.
Wie schnell steigt dieser in dem
Augenblick, in dem das Wasser 10 cm hoch steht? 2P
e) Wie viel Wasser ist dann im Behälter? 1P
VP |
30-29 |
28-27 |
26 |
25-24 |
23 |
22-21 |
20 |
19-18 |
17 |
16-15 |
14 |
13-12 |
11-10 |
9-8 |
7-6 |
5-0 |
|
NP |
15 |
14 |
13 |
12 |
11 |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
Klausur Nr. 2 Kurs 12
1) Bestimmen Sie das Integral
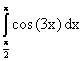. 3P
2) Wo steckt der Fehler?
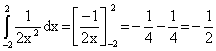. Zeigen Sie formal
sauber, dass der Flächeninhalt
zwischen dieser Kurve, x = –2, x = 2 und der x-Achse unendlich groß ist. 3P
3) Der Kelch eines Sektglases ist 4 cm hoch und die halbe Silhouette genügt der Gleichung
y = 
(grobe Skizze
genügt). Welches Volumen hat der Kelch? 3P
4) Gegeben sei die Funktion f mit f(t) = at2 + bt + c; a,
b, c, t 
.
Eine ihrer
Stammfunktionen ist
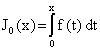
Das Schaubild dieser Stammfunktion hat den
Tiefpunkt T(0ï0), den Hochpunkt H(4ï2) und den Wendepunkt W(2ï1). Skizzieren
Sie grob dieses Schaubild und bestimmen Sie die Gleichung f(t) der Funktion f. 5P
Wahlteil mit Formelsammlung und GTR:
5) Wachstumsmodell I:
Eine 75 mm lange Liane wächst in den nächsten 50 Tagen in etwa linear ansteigend
von 20 auf 45 mm/Tag und anschließend in 40 Tagen in etwa linear fallend auf 0.
a) Bestimmen Sie die Gleichung der Wachstumsgeschwindigkeit w(t) in mm/Tag. 4P
b) Wie lang ist die Liane am Schluss dieses Wachstumsprozesses?
Protokollieren Sie dabei, was Sie in den GTR eingeben. 4P
c) Wie viele mm wächst die Pflanze durchschnittlich pro Tag in diesem
Beobachtungszeitraum? 1P
d) Warum lässt sich mit diesen Daten kein gesamtdurchschnittliches Wachstum pro Tag
angeben? 1P
Wachstumsmodell II:
Angenommen, die Liane wäre von Anfang an mit der im Wachstumsmodell I
beobachteten Geschwindigkeit w(t) gewachsen, also in etwa linear ansteigend von
0 auf 45 mm/Tag und die letzten 40 Tage in etwa linear fallend auf 0.
e) Wie viele Tage wäre sie dann gewachsen? Wie lang wäre sie am Schluss dieses
Wachstumsprozesses gewesen? Wie viele mm wäre die Pflanze durchschnittlich pro
Tag gewachsen? 4P
f) Welche Anfangslänge an Stelle der 75 mm hätte die Liane im Wachstumsmodell I
haben müssen, damit die beiden Wachstumsmodelle übereinstimmten? 2P
VP |
30-29 |
28-27 |
26 |
25-24 |
23 |
22-21 |
20 |
19-18 |
17 |
16-15 |
14 |
13-12 |
11-10 |
9-8 |
7-6 |
5-0 |
|
NP |
15 |
14 |
13 |
12 |
11 |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
Klausur Nr. 3 Kurs 12
Pflichtteil ohne GTR und Formelsammlung:
1 a) Berechnen Sie im Parallelogramm ABCD mit den Eckpunkten A(–3/2/3), B(–6/5/–9) und
C(4/0/7) die Koordinaten von D. 4P
b) Berechnen Sie den Mittelpunkt seiner Diagonalen. 1P
c) Gibt es ein a 
, so dass die Gerade (AB) und
,
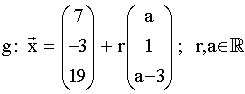parallel sind? Beweisen Sie Ihre Vermutung. 4P
d) Beweisen Sie allgemein, dass ein Parallelogramm ABCD im IR3 nie 4 linear unabhängige
Ortsvektoren besitzen kann. Unterscheiden Sie dabei, ob einer der Eckpunkte im
Ursprung sitzt oder nicht. 4P
Wahlteil mit Formelsammlung und GTR:
2) Gegeben sind die Punkte A(–3/2/3), B(–6/5/–9) und C(4/0/7).
a) Beweisen Sie, dass die Ortsvektoren von A, B, und C linear unabhängig sind.
Geben Sie Ihre Anfangs- und Endmatrix an. 3P
b) Berechnen Sie die Länge des
Vektors 
.
2P
3) Durch die Punkte A(2/1/0), B(8/7/–3) und C(5/5/–1) wird eine Ebene bestimmt.
a) Bestimmen Sie eine Parameterdarstellung und eine Koordinatengleichung der
Ebene. Überprüfen Sie, ob D(–4/–7/2) in dieser Ebene liegt. 5P
b) Bestimmen Sie die Schnittpunkte der Ebene mit den Achsen. Zeichnen Sie die
Ebene in ein Koordinatensystem und bestimmen Sie jeweils eine Parameterdarstellung
ihrer Spurgeraden s12, s13, s23. 7P
VP |
30-29 |
28-27 |
26 |
25-24 |
23 |
22-21 |
20 |
19-18 |
17 |
16-15 |
14 |
13-12 |
11-10 |
9-8 |
7-6 |
5-0 |
|
NP |
15 |
14 |
13 |
12 |
11 |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
Klausur Nr. 4 Kurs 12
Pflichtteil ohne GTR und Formelsammlung:
1) Gegeben sind die Punkte A(–1ï–1ï–1), B(5ï6ï5), C(7ï12ï14) und D(1ï5ï8).
Zeigen Sie, dass die Punkte A, B, C, und D in einer Ebene liegen und eine Raute, aber
kein Quadrat bilden. 8P
2) Die Ebene geht durch den Punkt P(4ï–2ï1) und ist orthogonal zur Geraden
.
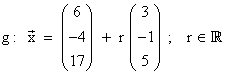Stellen Sie eine Koordinatengleichung der Ebene E auf. 2P
3) Die Gerade g durch den Punkt P(5ï0ï7) ist orthogonal zur Ebene E mit der Gleichung
2x1 + 5x2 + x3 = 37. Bestimmen Sie den Durchstoßpunkt. 3P
Wahlteil mit Formelsammlung und GTR:
4) Überprüfen Sie die Lage der Geraden. Bestimmen Sie gegebenenfalls Schnittpunkt
und Schnittwinkel der Geraden
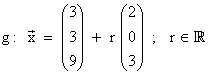
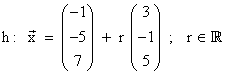5P
5) Die Punkte A(2ï–1ï–6), B(18ï–1ï6), C(–7ï–1ï6) und S(2ï7ï8) bilden eine dreiseitige
Pyramide mit der Spitze S.
a) Bestimmen Sie die Seitenlängen und Innenwinkel des Dreiecks ABC. 5P
b) Bestimmen Sie das Volumen dieser Pyramide. 6P
c) Begründen Sie mit eigenen Worten, warum dieses Dreieck parallel zur
x1x3-Ebene ist. 1P
VP |
30-29 |
28-27 |
26 |
25-24 |
23 |
22-21 |
20 |
19-18 |
17 |
16-15 |
14 |
13-12 |
11-10 |
9-8 |
7-6 |
5-0 |
|
NP |
15 |
14 |
13 |
12 |
11 |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
Klausur Nr. 1 Kurs 13
Pflichtteil ohne GTR und Formelsammlung:
1) Leiten Sie einmal ab und geben Sie eine Stammfunktion von f an:
a)
3P b) 
2P
2) Leiten Sie einmal ab: f(x) = 0,5x–1· e–2x 2P
3) Berechnen Sie das Integral.
a)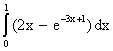 
b) 
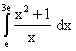je 2P
4) Eine Bazillenart verdreifacht sich jede halbe Minute.
Nach wie vielen Sekunden
hat sie sich verzehnfacht? Leiten
Sie eine Formel für t in sec her. 2P
Wahlteil mit Formelsammlung und GTR
(Genauigkeit auf 2 Dezimalen gerundet, kurz verwendetes GTR-Menü angeben):
5) Die Bevölkerungszahl der Länder A und B entwickeln sich gemäß nachfolgender Tabelle:
|
Jahr
|
1986 |
1991 |
1996 |
2001 |
2006 |
|
Einwohnerzahl
Land A in Mio. |
40,3 |
43,7 |
47,4 |
51,3 |
55,6 |
|
Einwohnerzahl
Land B in Mio. |
67,2 |
62,4 |
57,9 |
53,7 |
49,8 |
a) Um wie viel % etwa jährlich verändern sich die Einwohnerzahlen der beiden Länder? 2P
b) Wann hat Land A 80 Millionen Einwohner? 1P
c) Wann nimmt die Einwohnerzahl des Landes B um 0,5 Millionen pro Jahr ab? 2P
6) In einem neu angelegten Teich werden 350 Fische eingesetzt. Sie können sich zunächst
ungestört vermehren. Nach 3 Jahren wird geschätzt, dass 800 Fische in dem Teich leben.
a) Wie groß ist die Wachstumskonstante k auf 4 Dezimalen gerundet, wenn man exponentielles
Wachstum B(t) = c × e kt für t Jahre annimmt? 2P
b) Welcher Fischbestand ist 1 Jahr nach dem Einsetzen zu erwarten? 1P
c) Um wie viel % etwa jährlich wächst der Fischbestand nach diesem Modell? 2P
d) Wann wächst er um 100 Fische pro Jahr? 2P
e) Vier Jahre nach dem Einsetzen zeigt sich, dass der Platz für so viele Fische nicht
ausreicht. Der Bestand nimmt ab. Die Wachstumskonstante ändert sich in k = -0,15.
Welcher exponentiellen Gleichung genügt der Fischbestand ab da
und wie
groß ist er 7 Jahre nach dem
Einsetzen? 3P
f) Hätte man am Anfang weniger Fische eingesetzt, so wäre im Teich ein Wachstum
der Form
möglich gewesen.
Wie viele Fische hätte man also einsetzen müssen und welcher Fischbestand wäre nie
überschritten worden? 2P
VP |
30-29 |
28-27 |
26 |
25-24 |
23 |
22-21 |
20 |
19-18 |
17 |
16-15 |
14 |
13-12 |
11-10 |
9-8 |
7-6 |
5-0 |
|
NP |
15 |
14 |
13 |
12 |
11 |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
Klausur Nr. 2 Kurs 13
Pflichtteil ohne GTR und Formelsammlung:
1) Lösen Sie folgende Gleichungen nach x auf:
a) ln(x) – ln(
) = 1 2P b) 2ex – 8e–x = 6 5P
2) Leiten Sie einmal ab und geben Sie eine Stammfunktion von f an:
6P
Wahlteil mit Formelsammlung und GTR
(Genauigkeit beim Endergebnis auf 2 Dezimalen gerundet, kurz verwendetes GTR-Menü angeben):
3) Ein Fieberthermometer zeigt eine Zimmertemperatur von 20° C an. Nach 15 Sekunden
Fiebermessen bei einem Kranken misst man 25,2° C. Wie lange dauert es, bis eine
Fiebertemperatur von 39° C auf 0,1° C genau angezeigt wird? 5P
4) Im Modell kann die Wachstumsgeschwindigkeit einer Fichte
in Abhängigkeit
von der Zeit t näherungsweise durch
die Funktion w beschrieben werden mit
, wobei t in Jahren
und w(t) in Metern pro Jahr
angegeben wird. Beschreiben Sie kurz
Ihre Lösungswege und die dazu von Ihnen im
GTR gewählten Menüs.
a) Wann ist die Wachstumsgeschwindigkeit ebenso groß wie im 50. Wachstumsjahr? 5P
b) Wann ist diese
Wachstumsgeschwindigkeit erstmals unter 10 cm pro Jahr und
welche Höhe hat dann die Fichte?
4P
c) Geben Sie eine Funktion des beschränkten Wachstums für die Höhe an, wenn man
davon ausgeht, dass diese Fichte zum Zeitpunkt ihres schnellsten Wachsens 19,96 m
groß war und sie knapp unter 50 m bleiben wird. 3P
(Achtung: Diese Fichte wächst anfangs nicht nach dem Gesetz des beschränkten
Wachstums. Verwenden Sie daher als weitere Angaben Ihre Werte aus Teilaufgabe b.)
VP |
30-29 |
28-27 |
26 |
25-24 |
23 |
22-21 |
20 |
19-18 |
17 |
16-15 |
14 |
13-12 |
11-10 |
9-8 |
7-6 |
5-0 |
|
NP |
15 |
14 |
13 |
12 |
11 |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
Klausur Nr. 3 Kurs 13
Pflichtteil ohne GTR und Formelsammlung:
1) Bestimmen Sie den Grenzwert, falls er existiert, von
a) 
b) 
c) 
je 1P
2) Bestimmen Sie den Grenzwert, falls er existiert, von
a) 
b) 
je
2P
c) 
6P
Wahlteil mit Formelsammlung und GTR
(Genauigkeit beim Endergebnis auf 3 Dezimalen gerundet, kurz verwendetes GTR-Menü
angeben):
3) Für a 
\{0} ist die Funktion g gegeben durch g(x) = sin(ax) ; x 
.
a) Bilden Sie die erste, dritte und fünfte Ableitung von g. 2P
oder? Bilden Sie die erste bis sechste Ableitung von g.
b) Beweisen Sie durch vollständige Induktion, dass für die ungerade
(2n+1) te Ableitung g(2n+1) gilt:
g(2n+1) (x) = (–1)n · a2n+1 ·
cos(ax) ; n 
0. 7P
4) Ein Land hat zur Zeit 55 Millionen Einwohner und jährlich einen Bevölkerungsschwund
von 0,8% und 320 000 Einwanderer zu verzeichnen.
a) Auf welche Einwohnerzahl pendelt sich dieses Modell ein? (vgl. Kl. 10) 2P
b) Welche
Einwohnerzahl hat das Land 20 Jahre später?
(mit Mode Seq) 2P
c) Stellen Sie eine Differentialgleichung auf, mit der sich näherungsweise diese
Entwicklung der Einwohnerzahl beschreiben lässt und geben Sie die zugehörige
Wachstumsfunktion an. Welche Einwohnerzahl hat das Land nach diesem Modell
20 Jahre später? (mit Mode Func) 4P