Klassenarbeit Nr.1        Klasse 8

 

Pflichtteil ohne GTR:

 

1) Berechne den Schnittpunkt der Geraden y = x – 3 und y = x + .                                   2P

 

2) Löse das lineare Gleichungssystem rechnerisch:                      8x + 14y = 42

                                                                                                   3x – 4y = 25                      3P 

3) Wie lautet das Lösungspaar (x;y)?

     a)  2x + 4 = 3y für y = 4             und           b)         x = –y + 1 für x = –3               je 1P

4) Wie lauten die zugehörigen Geradengleichungen?                                                    4P

    

 

Wahlteil: GTR erlaubt, (kurz Menüs angeben),
erforderliche Genauigkeit: an der zweiten Stelle hinter dem Komma richtig gerundet

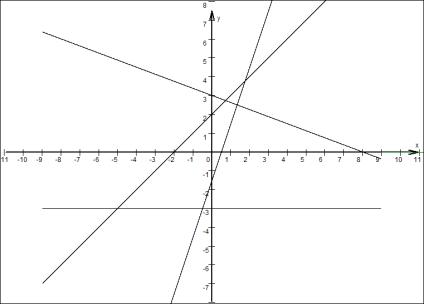
5) Berechne den Schnittpunkt der Geraden y = –x + 5 und y = x + .     

    Gib das Ergebnis in Brüchen an.                                                                                         2P

 

6) Löse die linearen Gleichungssysteme mit dem Matrix- oder GRAPH-Menü:

    Gib die Matrix oder die Geradengleichungen, die Du eingibst, an.

     a) 5x – 6y = 8         b) 3x – 17y = 18            c) x = –2(y – 3)      d) x = –4y + 5

         6x + 9y = 15           8y – 11x =  –66          171= –12y –6x          x = 0,9y – 1
    Gib das Ergebnis wenn möglich in Brüchen an.                                           a) 2P, sonst  je 3P

 

                                                                                                

Klassenarbeit Nr.2        Klasse 8

GTR darf von Anfang an verwendet werden, aber einfachste Wurzeln und Brüche
bitte stehen lassen.

 

1) Konstruiere samt Planfigur und kurzem Konstruktionstext ein Dreieck ABC aus:

    a)   a = 5,5 cm  ,    a = 46° ,   b =  63°                                                                             4P

    b)   a = 6,9 cm  ,   c = 4,3 cm ,   g = 32°                                                                           6P

    c)  Begründe mit einem Kongruenzsatz, warum das Dreieck aus a) eindeutig
         konstruierbar ist und das aus b) nicht.                                                                            2P

 

2) Ermittle zeichnerisch die Höhe einer Pyramide mit quadratischer Grundfläche mit

     a = 3,8 cm  und den Seitenkanten  s = 5,4 cm. (Tipp: zuvor grobe Schrägbildskizze)          3P

    

3) Konstruiere  durch ein geeignetes Quadrat.                                                                2P

 

4) Berechne und lasse die einfachsten Wurzeln stehen.                                                            7P

    , ,  mit a > 0,  

 

Klassenarbeit Nr.3        Klasse 8

 

Pflichtteil ohne GTR:

 

1) Multipliziere aus und fasse soweit wie möglich zusammen (binomische Formeln erlaubt)

     (b + 2)2 - (3 - b)2                                                                                                            3P                    

2) Klammere aus und ermittle, für welche Werte der Term den Wert 0 annimmt

    5b3 - 50b2                                                                                                                        2P                                          

3) Bestimme den Scheitelpunkt von der Parabel  y = 2x – 4x2                                                 2P                              

4)  Gegeben sind die Punkte A(0ï5), Scheitelpunkt S(2ï–3) und C(4ï5).

     Leite die zugehörige Parabelgleichung in Scheitelform her.                                      2P

 

5) Bestimme die Lösungsmenge der Gleichung    z2 - 8z + 16 = 0                                          2P

 

 

Wahlteil: GTR erlaubt, (kurz Menüs angeben),
erforderliche Genauigkeit: an der zweiten Stelle hinter dem Komma richtig gerundet

 

6)  Bestimme die Scheitelpunkte der Parabeln

     a) y =  x2 – 2,4x +                  1P        b)  y =   –x2 + 3,6x –1,2                              1P                                          

7) Ein Schäfer will für seine Schafherde einen rechteckigen Pferch machen. Er hat dazu
    50 m Zaun zur Verfügung. Wie muss er die Maße des Rechtecks wählen, damit für
    eine Umzäunung ein möglichst großer Pferch entsteht, wenn eine Rechteckseite von

    einem Bach gebildet wird?   Skizze empfehlenswert.                                                          6P

 

8) Bestimme die Lösungsmenge der Gleichung    4x2 + x - 14 = 0                              2P

 

9) Löse  =                                                                                               3P

 

 

Klassenarbeit Nr.4        Klasse 8

 

Rechenwege angeben und ausgerechnete Brüche stehen lassen.

 

Pflichtteil ohne GTR:

 

1) In einer Urne sind zwei  rote, drei grüne und vier blaue Kugeln.
    Es werden nacheinander drei Kugeln gezogen und jeweils auf den Tisch gelegt.

    Bestimme die Wahrscheinlichkeiten für

    a) „ zuerst werden zwei grüne und dann eine rote Kugel gezogen“                           2P

    b) „alle gezogenen Kugel sind rot“                                                                          1P

    c) „beide rote Kugeln wurden gezogen, aber keine blaue“                                       2P
    d) „ es wurde höchstens zweimal blau gezogen“                                                                  2P

 

2) In einem Lostopf sind fünf Kugeln durchnummeriert von 1 bis 5.

    Es werden nacheinander drei Kugeln gezogen und jeweils wieder zurückgelegt.

    Bestimme die Wahrscheinlichkeiten für

    a) „ genau zwei Fünfer sind dabei“                                                                          3P

    b) „alle gezogenen Kugeln sind Einser“                                                                               1P

       

 

Wahlteil: GTR erlaubt,  Rechenwege angeben (evtl. kurz Menüs angeben),
erforderliche Genauigkeit: bei Prozentangaben an der zweiten Stelle hinter dem Komma richtig gerundet, sonst an der vierten Stelle.

Aus der Mitte des  Klassenarbeitsheftes die für den Wahlteil nötigen Blätter herauslösen.

 

3) Ein Schütze trifft mit einer Wahrscheinlichkeit von 87% ins Schwarze und

    schießt eine 8er-Serie.

    a) Erstelle eine Wahrscheinlichkeitsverteilung von 0 bis 8 Treffern.                           2P

    b) Mit welcher Wahrscheinlichkeit trifft er genau drei Mal?                                      1P
    c) Mit welcher Wahrscheinlichkeit trifft er höchstens vier Mal?                                            2P

    d) Mit welcher Wahrscheinlichkeit trifft er mindestens fünf Mal?                              2P

 

4) In einem Lostopf sind acht Kugeln durchnummeriert von 1 bis 8.

    Es werden nacheinander drei Kugeln gezogen und jeweils wieder zurückgelegt.

    Bestimme die Wahrscheinlichkeiten für

    a) „ genau zwei Fünfer sind dabei“                                                                          3P

    b) „alle gezogenen Kugeln sind Einser“                                                                               1P

 

5) In einem Lostopf sind zehn Kugeln durchnummeriert von 1 bis 10.

    Es werden nacheinander drei Kugeln gezogen und nicht wieder zurückgelegt.

    Bestimme die Wahrscheinlichkeit für „ genau eine gerade Zahl ist dabei“.                 2P