Klassenarbeit  Nr. 1

 

1) Begründe mit Hilfe der Teilbarkeitsregeln, welche Zahlen durch 3, 4, 5, 6, 8, 9

    und 15 teilbar sind.                   a) 3 592         b) 4 275        c)  1 430                                6P      

 

2) In nachfolgenden Mengen fehlen ein paar Zahlen, damit sie zu einer echten

    Teilermenge werden. Ergänze die fehlenden Zahlen, so dass Du die Teilermenge

    einer bestimmten Zahl erhältst. Um welche Zahl handelt es sich? Wie lautet die 

    dazugehörige  Teilermenge?

    a)  {1; 2; 4; 38; 76}                   b)  {1; 2; 3; 4; 5; 10; 12; 20; 30}                                   4P

 

3)  Von welcher Zahl ist dies die Vielfachmenge?  Füge davor und danach die passende Zahl an.

  

       =  {...;         ; 68; 102; 136;         ;  ...}          =  {...;        ; 81; 108; 135;        ; ...}        4P

 

4) Berechne

     a) kgV (136; 712)  b) kgV (24; 27)   c) ggT (126; 144)       d) ggT ( 74;  480)              8P

 

5) Von welchen unbekannten Zahlen x ist kgV (x; 9)  =  45. Sammle.                          2P

 

 

Klassenarbeit  Nr. 2         Klasse 6

 

  1)  Zeichne die Winkel mit der Winkelweite a = 63°,  b = 142°, g = 217° und  d = 273°.                 4P

 

  2) Zeichne den Scheitelwinkel zum Winkel mit  a = 67° .                                                                       1P

 

  3) Zeichne den Nebenwinkel zum Winkel mit  a = 74° .                                                                         1P

 

  4) Zeichne einen Zahlenstrahl. (Beginne mit 0 und wähle die 1 bei 6 cm.) Trage ein:

     ;   ;   ;   und   .                                                                                                                               3P

 

  5)  Schreibe als Rechenausdruck und berechne:  

 

    a)    von 240 kg,                                                    b )   von 145 DM                                                     2P

 

  6) Ein Mensch besteht zu etwa 13% aus Blut. Wieviel Liter Blut hat ein Schüler mit 46 kg?       2P

 

  7) Kürze soweit wie möglich:    ;    .                                                                                         3P

 

  8) Erweitere auf den Hauptnenner:    ;  .                                                                                          1P

  

  9)  Bilde den Hauptnenner und ordne der Größe nach:   ;   ;   .                                          4P

 

10) Addiere und kürze, falls möglich :   ;          .                                                              3P

 

Klassenarbeit  Nr. 3         Klasse 6

 

(zu leicht ohne Textaufgaben)

Kürze soweit wie möglich und gib das Ergebnis möglichst als gemischte Zahl an.

 

1)          2P;     2)     3P;    3)     von   m     2P;

 

 

4)      3P;   5)      4P;

 

 

6)       5P;

 

 

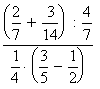7)      5P;

 

 

Klassenarbeit  Nr. 4         Klasse 6

 

1)  a) Spiegle das Dreieck ABC mit A(2ï1), B(4ï2) und C(4ï5) an der Geraden PQ durch

         die Punkte P(1ï5) und Q(5ï1).                                                                                                               4P

     b) Drehe das Dreieck um A mit a = 20°.                                                                                                  2P

     c) Verschiebe das Dreieck so, dass A’(3ï0) der Bildpunkt von A ist.                                             2P

 

2) Schreibe mit Bruchstrich und kürze dann so weit wie möglich: 0,0125                                         1P

 

3) Kürze oder erweitere zunächst und schreibe dann mit Komma:                                               2P

4) Schreibe mit Komma in der nächstgrößeren Einheit:  46 mg                                                            1P

 

5) Runde a) auf Zehntel, b) auf Hundertstel, c) auf Tausendstel: 0,6645                                             3P

 

6) Berechne a) 938,91 + 0,95 - 2,02     b) 370,7 × 0,057       c) 4,653 : 11                                                  je 2P

 

7) Multipliziere die Summe der Zahlen 84,3 und 146,9 mit ihrer Differenz.                                          3P

 

 

Klassenarbeit  Nr. 5         Klasse 6

 

1) Wer ist im Mittel schneller: Ein Schüler, der auf 50 m 8 s braucht oder ein Schüler,

     der in einer Viertelstunde  mit dem Fahrrad  5 625 m zurücklegt.?                                                  4P

 

2)  Die Renovierung einer Schule kostet  14,25  Mio. DM. Das Land trägt zwei Fünftel der Kosten,

     die Stadt den Rest. Wieviel muss jeder bezahlen?                                                                              3P

 

3) Eine volle Flasche Mineralwasser wiegt  2,8 kg. Die leere Flasche wiegt 2,05 kg. Gib das  

    Gewicht des Inhaltes als Bruchteil vom Gesamtgewicht an.                                                              3P

 

4) Die Apfelernte eines Bauern wird in 1 400 „l“ - Flaschen abgefüllt.

    Wie viele „l“ - Flaschen hätte dies ergeben?                                                                                     4P                                  

5) Von 152 Schülern eines Jahrgangs lieben 95 Schüler das Fach Mathematik. Berechne ihre

     relative Häufigkeit und wandle in Prozent um.                                                                                      3P

 

6) Ein Schwimmbecken fasst 5 642 l Wasser. In 6½ h füllt eine Leitung das Becken. Eine zweite 

    bräuchte dazu 5h 10 min.

     a)  Wie viel m3 Wasser liefert jede Leitung für sich genommen pro Stunde?                                3P

     b) Wie lange dauert es ungefähr, bis das Becken durch beide Leitungen zusammen gefüllt ist?  

          Runde auf 2 Stellen hinter dem Komma.                                                                                            4P

 

Klassenarbeit  Nr. 6         Klasse 6

 

1) Eine Münze hat einen Durchmesser von 2,1 cm. Berechne Ihren Umfang und ihren

    Flächeninhalt mit Hilfe von p =  .                                                                                                          4P

2) Berechne 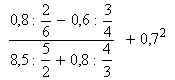.                                                                                                            6P

 

3) Ein Flugzeug steigt vom Moment des Abhebens bis zum Erreichen der Reiseflughöhe in jeder  

    Sekunde um die gleiche Anzahl von Metern nach oben. Nach 12,5 Minuten hat es auf  diese

    Weise eine Höhe von  4 200 m über dem Startpunkt erreicht. In welcher Höhe befindet es sich

    17,5 Minuten nach dem Abheben?                                                                                                            3P

 

4)  Ein Trinkwasservorrat einer Segeljacht ist so bemessen, daß er für 15 Personen 42 Tage

     ausreicht.

     a) Wie viele Personen dürfen an Bord sein, wenn der Vorrat 35 Tage ausreichen soll?           2P

     b) Die Jacht sticht mit 15 Personen in See. Nach 30 Tagen werden bei einer Zwischenstation

         weitere 5 Personen an Bord genommen. Wieviel Tage insgesamt reicht unter diesen

         Umständen der Trinkwasservorrat? (Es wird angenommen, daß jede Person an jedem Tag 

         gleich viel Trinkwasser verbraucht.)                                                                                                    5P

           

5)  Ein  25 cm langes,  24 m breites rechteckiges Kupferblech wiegt  267 g. 1 cm3 Kupfer

     wiegt 8,9 g. Berechne die Dicke des Kupferblechs.                                                                             4P